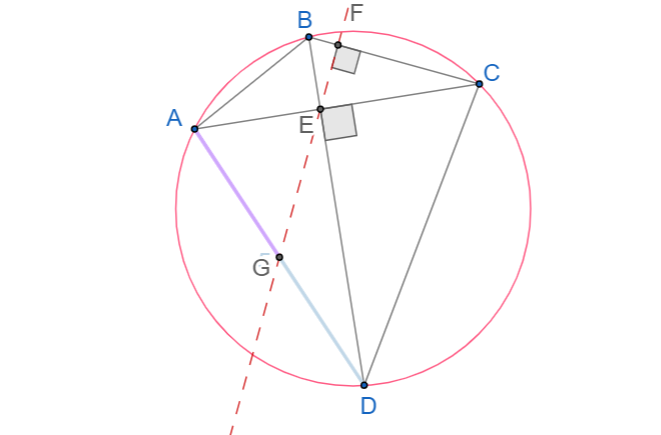
Теорема.
Если вписанный четырехугольник имеет перпендикулярные диагонали, то прямая проходящая через точку пересечения диагоналей, перпендикулярно какой-нибудь стороне четырехугольника делит противоположную ей сторону пополам.
Доказательство.
Так как ∠EAD + ∠EDA=90º, ∠FEC + ∠FCE=90º(свойство прямоугольного треугольника) и ∠ADB=∠ACB (вписанные углы, опирающиеся на дугу AB), то ∠EAD=∠FEC.
∠FEC=∠AEG (свойство вертикальных углов).
Следовательно, треугольник GAE является равнобедренным.
Аналогично доказывается, что треугольник GED — равнобедренный.
Следовательно, AG=EG=GD.